Leetcode: 一个思路对付所有的stock系列
首先需要说明的是,这个思路对stock系列是一个共同的切入点,并且都可以AC,但不代表是最优的解法,还需要优化。
Leetcode到目前为止一共有四个关于股票的题目,分别是:
Best Time to Buy and Sell Stock
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Best Time to Buy and Sell Stock II
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times). However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
Best Time to Buy and Sell Stock III
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete at most two transactions.
Note: You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
Best Time to Buy and Sell Stock IV
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete at most k transactions.
Note: You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
四个题目的共同点:已知条件都是一段时间内的股票价格走势,都是不允许同时进行多手交易,都是求最大收益。 区别在于交易次数(或者说频率)的限制。
I:只能交易一次;
II:可以交易多次;
III:只能交易两次;
IV:至多交易k次;
思路:
股票收益最简单的道理就是低价买高价卖(买空),如果现在手里并没有持有股票,仅针对这一简单原则执行即可,不需要考虑持有的股票在买卖区间内的价格波动。如果现在手里正持有股票,股价下跌的区间同样可以用来收益,先选一个高点卖出,再在之后的低点买进,手里的股票没有变,多了一次差价的收益(卖空);也可以理解为把一次交易给拆分成两次来做,避开了其中最大跌幅的区间。
首先我们一定是从买空开始操作的,在买空后,我们要找的是未持有股票区间内的最大买空收益(也就是涨幅)或持有股票区间内最大卖空收益(也就是跌幅)。
如果要区分标记这两种区间还是比较麻烦的,这里就是关键:为了计算简便,我们把求卖空转为求买空。买空寻求的是最大涨幅,卖空寻求的是最大跌幅。只要我们把需要求卖空的区间反转一下,最大跌幅就变成了最大涨幅,求卖空就变成了求买空。
最后还有一个小问题需要处理,反转以后容易在反转的边界处产生一个不存在的收益。如图所示:
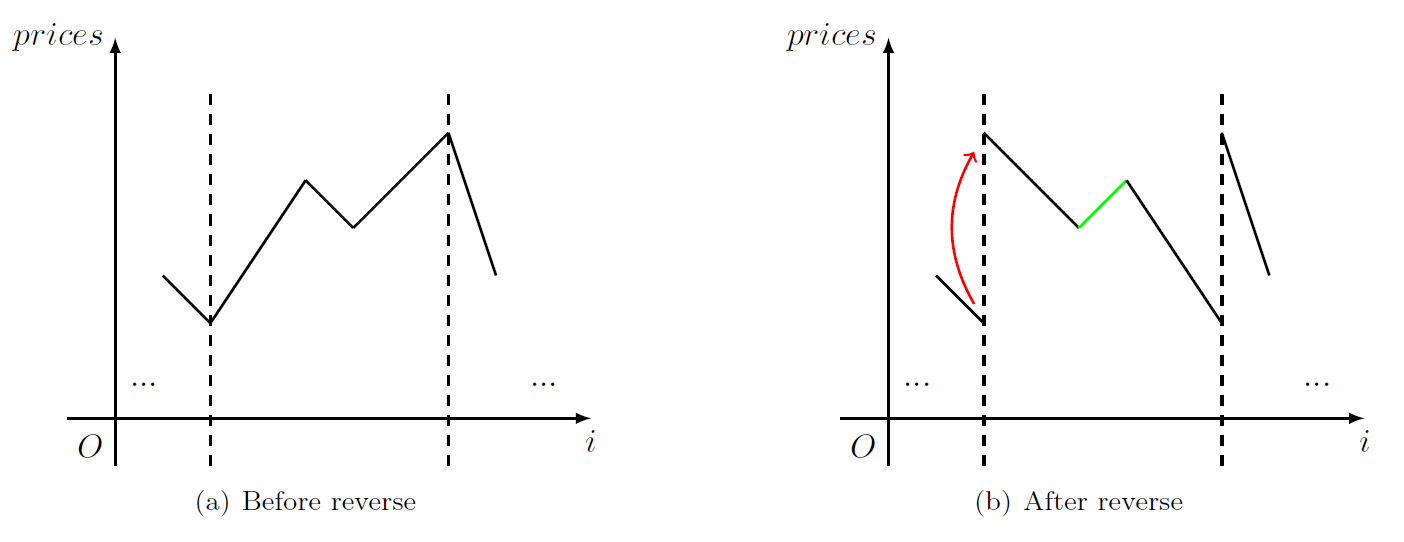
其中右图绿色线段标出了反转以后新的可收益时间段,红色箭头标出了不存在的收益。
为了标记边界,我们把反转的区间两段标上一个特殊值。因为股票的价格都是非负值(其实我觉得0也不太可能),特殊值可以选为-1。
所以,我们可以先写出一个基本的函数,求下一次的最大收益:
int nextMaxProfit(vector<int>& prices){
if(prices.size() < 2) return 0;
int len = prices.size(), minval = prices[0], profit = 0, minpos = 0, maxpos = 0, minposnow = 0;
for(int i = 0; i < len; ++i){
if(prices[i] == -1 && i < len - 1){
minval = prices[i+1];
minposnow = i+1;
}else if(prices[i] < minval){
minval = prices[i];
minposnow = i;
}else if(prices[i] - minval > profit){
profit = prices[i] - minval;
maxpos = i;
minpos = minposnow;
}
}
prices[minpos] = prices[maxpos] = -1;
reverse(prices.begin()+minpos, prices.begin()+(++maxpos));
return profit;
}然后只要按照题目逻辑运用即可:
// I: 8ms
class Solution {
public:
int maxProfit(vector<int>& prices) {
return nextMaxProfit(prices);
}
};
// II: 16 ms
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ret = 0;
while(true){
int profit = nextMaxProfit(prices);
ret += profit;
if(profit == 0) break;
}
return ret;
}
};
// III: 8 ms
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ret = nextMaxProfit(prices);
return ret == 0 ? 0 : ret + nextMaxProfit(prices);
}
};
// IV: 712 ms
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int ret = 0;
while(k--){
int profit = nextMaxProfit(prices);
ret += profit;
if(profit == 0) break;
}
return ret;
}
};复杂度方面,每求一次nextMaxProfit都是O(n),所以对于I和III这种只求很少几次交易的题目,复杂度都是O(n),速度还是比较不错的。不限制交易次数的话,最坏的情况是要执行n/2次交易,复杂度将会变成O(n^2)。IV的复杂度也会达到O(kn)。可以看到在求IV时,速度已经不能令人满意了(II表现还好而IV表现差我猜可能是测试用例的关系)。总之,希望这个思路能给在求这类题目时寻找线性解法一个启发。
所以说,了解了解生活中的常识对编程还是有帮助的,不是么。