Range Sum Query 2D - Immutable

figure

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

Note:

You may assume that the matrix does not change.

There are many calls to sumRegion function.

You may assume that row1 ≤ row2 and col1 ≤ col2.


这道题的思路可以基于Range Sum Query - Immutable展开。Range Sum Query - Immutable是一维的数组，这里扩展成二维，所以需要把整个平面分成四个空间：

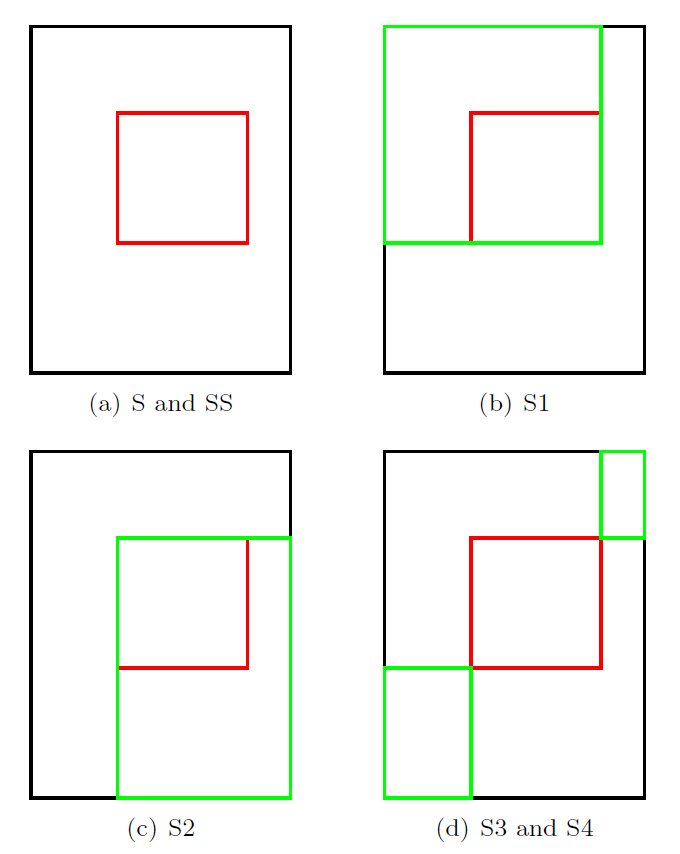
figure

假设图(a)中，整个矩阵里所有元素的和为SS，待求的部分元素（红色矩阵）的和为S，图(b)，图(c)和图(d)中绿色矩阵的和分别为S1，S2，S3和S4，则有：

S = S1 + S2 + S3 + S4 - SS

顺着这个思路来，需要维护四个matrix分别记录(i, j)位置和四个角分别所构成的矩形中元素的和。

代码：

class NumMatrix {
public:
    NumMatrix(vector<vector<int>> &matrix) {
        m = matrix.size();
        n = m == 0 ? 0 : matrix[0].size();
        sum = 0;
        int linesum = 0;
        if(m != 0 && n != 0){
            for(int i = 0; i < m; ++i){
                lt.push_back(vector<int>(n, 0));
                linesum = 0;
                for(int j = 0; j < n; ++j){
                    linesum += matrix[i][j];
                    sum += matrix[i][j];
                    if(i > 0) lt[i][j] = linesum + lt[i-1][j];
                    else lt[i][j] = linesum;
                }
            }
            for(int i = 0; i < m; ++i){
                rt.push_back(vector<int>(n, 0));
                rt[i][0] = lt[i][n-1];
                for(int j = 1; j < n; ++j) rt[i][j] = lt[i][n-1] - lt[i][j-1];
            }
            lb.push_back(lt[m-1]);
            for(int i = 1; i < m; ++i){
                lb.push_back(vector<int>(n, 0));
                for(int j = 0; j < n; ++j) lb[i][j] = lt[m-1][j] - lt[i-1][j];
            }
            rb.push_back(rt[m-1]);
            for(int i = 1; i < m; ++i){
                rb.push_back(vector<int>(n, 0));
                for(int j = 0; j < n; ++j) rb[i][j] = rt[m-1][j] - rt[i-1][j];
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        if(m == 0 || n == 0) return 0;
        return lt[row2][col2] + rb[row1][col1] + (row1 == 0 || col2 == n-1 ? 0 : rt[row1 - 1][col2 + 1]) + (row2 == m-1 || col1 == 0 ? 0 : lb[row2 + 1][col1 - 1]) - sum;
    }
    
    vector<vector<int> > lt, rt, lb, rb;
    int sum, m, n;
};

需要注意的是计算sumRegion时需要对右上和左下两块的和做一下判断，防止出现下标为-1的情况。新建数据结构的时间复杂度为O(mn)，sumRange的时间复杂度为O(1)，整个数据结构的空间复杂度为O(mn)。